A photovoltaic solar panel will generate the most electricity when solar radiation hits it directly – i.e. the sun’s rays are hitting the panel perpendicularly (i.e. at a 90 degree angle, face on). As the sun appears to move across the sky from east to west through the day, and it appears to move up and then down in the sky as well, an optimum fixed mounting position must be found for a solar array to collect the maximum amount of energy possible.

The Solar Spreading Out Effect

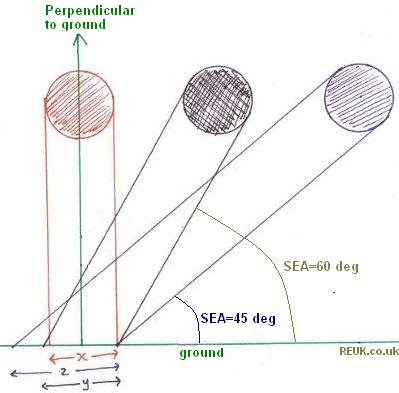
The diagram above demonstrates the solar spreading out effect. As the sun goes lower in the sky, the solar radiation hits the ground at an angle – the solar elevation angle (SEA). As the angle of the sun above the horizon goes down, the concentration of solar radiation hitting a unit area on the ground goes down too.

Imagine we have one square metre of sunshine hitting the Earth. When the sun is directly overhead (perpendicular to the ground), that one square metre will illuminate exactly one square metre on the ground. As the sun moves down toward the horizon, that same one square metre of sunshine will illuminate more than one square metre on the ground, but at a lower intensity since the same amount of solar radiation has been spread out over a larger area.
As the diagram above shows in one dimension, as the sun moves lower, the length of the illuminated area on the ground increases: x (perpendicular – 90 degree SEA) < y (60 degrees SEA) < z (45 degrees SEA).

Trigonometry Calculations of the Solar Spreading Out Effect

When it comes to solar panels what we want to know is how the angle the sun hitting the panel affects power output. Going back to our one-dimensional diagram and making some calculations, we can do exactly that:

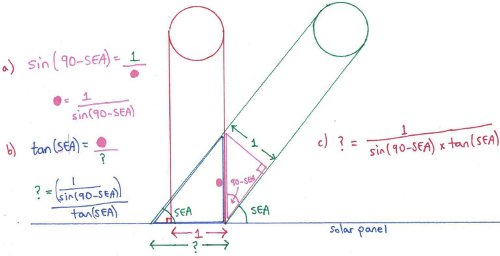
To keep things simple we have use a unit (1) width for the solar radiation hitting a solar panel located flat on the ground when the sun is perpendicular to the panel. First making the pink triangle, and then the blue, we find that the 1 unit width of the solar radiation hitting the solar panel is stretched when the sun is hitting the panel at the angle SEA to:

Putting some numbers into this equation, we see that if SEA is 60 degrees, the answer is 1.15. So, 1 unit length of solar radiation has been stretched to 1.15 units, or the amount of power that will be generated compared to when the sun was perpendicular is 1/1.15 = 0.87, a power reduction of 13%.

Solar Spreading Effect on Solar Panels

Of course in reality, almost no-one has their solar panels lying flat on the ground. They will instead typically be installed on a sloping roof, or on brackets which give the same pitch (aka tilt angle). Therefore, for real world scenarios we need to take into account the tilt angle of the solar panels when making these calculations.

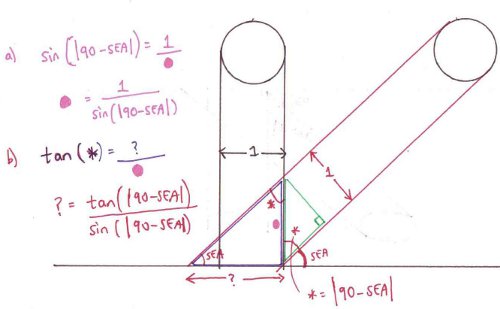
Above shows an alternative method of calculating the solar spread effect in one dimension. Note that this time the notation is a bit different – e.g. |90-SEA| where the || symbols indicate that we must turn any negative result into a positive result of the same magnitude – e.g. if SEA was 110, 90-110 is -20, but |90-110| is +20, the difference between the two angles.

Solar panels are fitted with a tilt angle in order to point the panels closer to the direction of the sun. Therefore we need to ADD the tilt angle to the solar elevation angle to get the angle that the sun is elevated from the solar panel – for example, if the tilt angle is 30 degrees, and the SEA is 20 degrees, we get 30+20 = 50 degrees (50 degrees from the solar panel face, 40 degrees from perpendicular).
If the tilt angle is instead 45 degrees (typical UK roof pitch) and the SEA is 60 degrees (noon on a summer’s day), then the result is 60+50 = 110 which is |90-110| = 20 degrees from perpendicular.

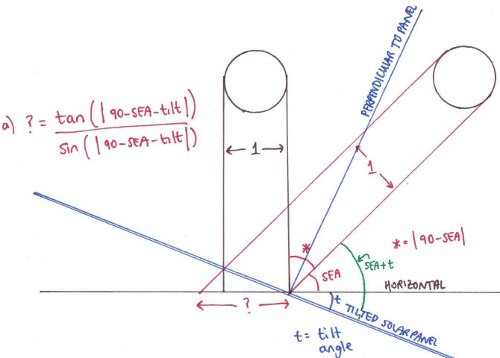
The above diagram shows how all this comes together in the final equation which takes into account the solar panel tilt angle as well as the solar elevation angle:

Putting some numbers into the final equation, we see that if the SEA is 15 degrees (UK winter at noon) and the tilt angle is 45 degrees, then the resulting width is:
tan (|30|)/ sin (|30|) = 1.154.
…and if the SEA is 15 degrees and the tilt angle is 60 degrees, then the resulting width is:
tan (|15|)/ sin (|15|) = 1.035.
…which proves that seasonal adjustment of solar panels increases power generation as increasing the tilt angle from the usual 45 degrees to 60 degrees in the winter results in 10% more generation.

Two Dimensional Power Calculations

All these calculations have so far been in one dimension focusing on the changing height of the sun in the sky and the tilt angle of the solar panel. There is of course a second factor – the sun moves across the sky from East to West. Fortunately the exact same equation can be used again to work out the effect of this movement across the sky.

Let’s say we have a solar panel installed facing due South with no longitudinal tilt, and the sun is shining in the South East. A line drawn perpendicular to the solar panel points due South, and the angle between it and South East is 360/8 = 45 degrees. The width of our one unit wide beam of solar radiation on the solar panel will therefore be equal to:
tan (|90-45|) / sin (|90-45) = 1.41, so we are getting 1/1.41 = 71% of the power we’d get if the sun were in the South.

When taking all the factors into account, we have solar spreading in the vertical direction and in the horizontal direction. Our perfect one square unit area of solar radiation therefore hits our angled solar panel as a rectangle whose size tells us how much power we are getting relative to the solar panel pointing directly at the sun.

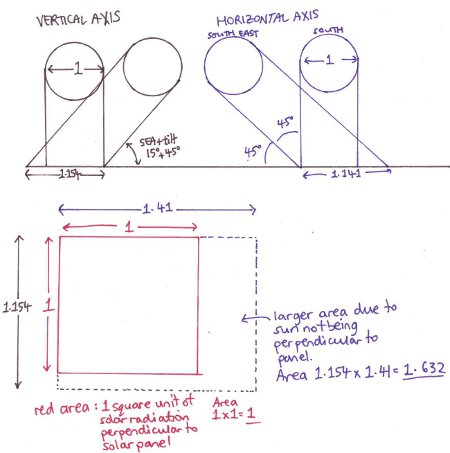
For example, if we have the sun at 15 degrees above the horizon and a tilt angle of 45 degrees, and the solar panel is installed facing due South, but the sun is in the South East, we multiply the two widths previously calculated to give us the area of the rectangle of sunlight hitting the solar panel:
1.154 * 1.41 = 1.632
…therefore in these conditions, the solar panel will generate 100 * (1/1.632) = 61.3% of the power it would have been generating if it were pointing directly at the sun. Such large losses in generation potential are why some people use solar trackers (discussed later in this article).

The Effect of the Atmosphere on Solar Generation

When the sun is low in the sky, in addition to the spreading out effect, solar radiation has to pass through a lot more of the atmosphere than when the sun is at its highest in the sky at noon. This further reduces the amount of solar radiation which gets to the solar panel – for example, by around 20% when the sun is 30 degrees above the horizon, and by 10% when the sun is 45 degrees above the horizon.

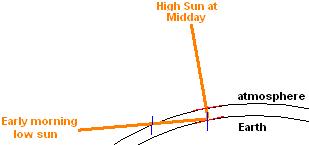
Here in the high latitudes of the UK, even in the South of England there are only a few days per year when the sun manages to get over 60 degrees at noon, and whole months when it doesn’t even get up to 15 degrees at noon meaning that more than 40% of the solar radiation is absorbed by the air massbefore it even gets to your solar panel at noon on a winter’s day. Sadly there is not a lot you can do about this short of moving your solar panels up a high mountain so that the solar radiation is only passing through the thin high atmosphere. (This will also give benefits thanks to the effect oftemperature on solar panels!)

For a lot more information on the Effect of Air Mass on Solar Panels click here.

Mounting Angle for Solar Panels

In general photovoltaic solar panels should be mounted at an angle of 10 to 15 degrees plus the site’s latitude. Therefore in London, which has a latitude of around 51 degrees, solar panels should ideally be mounted at an angle of approximately 65 degrees.

In the Northern Hemisphere, solar panels should face to the South where the sun is found at midday. Similarly in the Southern Hemisphere, solar panels should face to the North.

Seasonal Adjustment and Tracking

For all locations outside the tropics, if the panels are not fitted to a roof and cannot be moved, it is possible to greatly increase total annual power generation by adjusting the solar panel mounting angle through the seasons so that it is steeper during the winter when the sun is low in the sky, and more shallow during the summer when the sun is relatively high in the sky.

A solar tracker is a device which swings solar panels so that they follow the sun’s apparent motion across the sky during the day – either in one dimension from east to west, or in two dimensions from east to west and up and down. This can increase daily power output by as much as 30%, but it introduces mechanical components to the system which are liable to fail and require maintenance and it can also add considerable cost.

It normally does not make financial sense to use solar tracking with solar systems with a rated power output in excess of a few hundred Watts. Click here for more information on solar tracking, and here for details of a simple solar tracking concept.