In our article Solar Panel Mounting Angle we briefly touched on the effect of the atmosphere on the solar generation. As the Sun’s rays pass through the atmosphere, the energy of some photons of light is absorbed and scattered by particles in the atmosphere. The lower the Sun is in the sky (closer to the horizon), the thicker the layer of atmosphere the Sun’s rays must pass through to get to the solar panel down here on the Earth’s surface, and therefore the more energy is absorbed in the atmosphere which is therefore not available for the solar panel to convert into electricity.
The distance the Sun’s rays have to pass through the atmosphere can make a significant reduction in the amount of electricity which can be generated by a PV solar panel or the amount of hot water which can be made by a solar water heating system, particularly in higher latitudes such as here in the UK and especially in the winter months when the Sun is low in the sky all day.
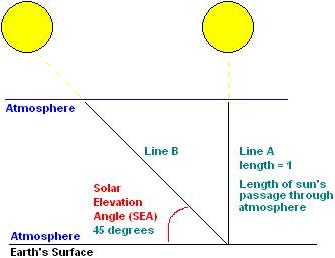
The above diagram illustrates this effect. Line A shows the Sun directly overhead. If the thickness of the atmosphere through which the Sun’s rays pass is given by 1 unit of length, we can work out the length of line B which shows the Sun at a solar elevation angle (SEA) of 45° above the horizon:
Therefore when the Sun is at an SEA of 45 degrees, the Sun’s rays pass through 41% more atmosphere than they would if the Sun were overhead (SEA = 90).
What is Air Mass
Air Mass is a measure of the amount of atmosphere the Sun’s rays have to pass through. Air mass is abbreviated to AM where the following notation is used: AM1 is the amount of atmosphere the Sun’s rays have to pass through when the Sun is directly overhead. This is the lowest possible AM value. In the example above where we had the Sun at 45° above the horizon, we write that we have AM1.41.
As the Sun moves closer to the horizon, the amount of air mass that it’s rays have to pass through starts to rapidly increase.
Here is a table of air mass for some values of solar elevation angle:
| SEA | Air Mass |
| 90° | AM1 |
| 60° | AM1.15 |
| 45° | AM1.41 |
| 30° | AM2 |
| 20° | AM2.92 |
| 15° | AM3.86 |
Once we get below a solar elevation angle of around 15-20°, this simple trigonometrical estimation of air mass becomes increasingly inaccurate since it ignores the curvature of the Earth. As the Sun get’s closer to the horizon, the following equation can be used:
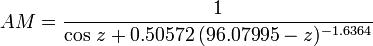
where z is (90 – solar elevation angle).
If the atmosphere is treated as a simple spherical shell, the above equation can be simplified to:
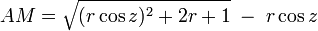
where again z is (90 – solar elevation angle), and r is the ratio the radius of the Earth (approx 6371km) to the depth of the atmosphere (9km since we can ignore the effect of the very thin atmosphere above that height without losing much accuracy). Therefore the value of r is approximately 708.
Using either of these equations, we see (approximately) that with an SEA of 10° we have AM5, at 5° we have AM10, at 2° we have AM20, and at 0° we have AM38. Therefore, when the Sun is say 2° above the horizon, the sunlight has to travel through 20 times more air mass than when the Sun is directly overhead.
Air Mass and Solar Insolation / Intensity
Solar Insolation is a measure of the amount of incident solar radiation (the solar intensity) directly hitting a given part of the Earth’s surface. It has to be measured rather than calculated since it depends on latitude, humidity, air pollution and smog, local weather, altitude, and even the shading effects of local mountains. (See our article Solar Insolation.)
Solar intensity is measured in W/m2 (Watts per square metre), and at AM1 (when the Sun is directly overhead) it is approximately 1040 W/m2 at sea level.
As the Sun moves down toward the horizon, the air mass value increases as shown earlier, and the solar intensity level falls – i.e. as the Sun moves lower in the sky, the amount of solar energy getting through the atmosphere and to ground level goes down as more energy is absorbed and scattered by particles in the atmosphere.
The relationship between air mass value and solar intensity has been modelled (experimentally determined) and the following equation gives a good approximation at sea level:
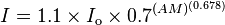
where AM is the air mass, Io is the intensity of the Sun hitting the top of the atmosphere (1.353 kW/m2), and I is the intensity of the Sun reaching a flat surface perpendicular to the Sun’s rays at sea level.
Trying different air mass values with this equation, it becomes clear that the effect of air mass on solar insolation is not significant when the sun is high in the sky. With AM1.15 (solar elevation angle 60°) the intensity is 1010 W/m2, less than a 3% drop from AM1 (Sun overhead). With AM1.41 (solar elevation angle 45°) the intensity is still 950 W/m2, only a 9% drop from AM1.
It is only when we get down below around 30° solar elevation angle that the effect of air mass becomes really significant, for example when the sun has moved down to just over 10° above the horizon, half of the energy of the Sun’s rays are lost on their way through the atmosphere.
| SEA | W/m2 | % Drop cf AM1 |
| 90° | 1040 W/m2 | 0.0% |
| 60° | 1010 W/m2 | 2.9% |
| 45° | 950 W/m2 | 8.7% |
| 30° | 840 W/m2 | 19.2% |
| 20° | 710 W/m2 | 31.7% |
| 15° | 620 W/m2 | 40.3% |
| 10° | 470 W/m2 | 54.8% |
| 5° | 270 W/m2 | 74.0% |
| 1° | 56 W/m2 | 94.6% |
Further Reading
For more information have a look at the following articles from external websites:
Calculating Relative Air Mass – Institute for Earth Science Research and Education.
Air Mass & Solar Energy – Wikipedia.
Solar Radiation – Wikipedia.